洛谷P2435 染色

学了好久忘光了，来补一发轮廓线DP

这道题有很显然的状压做法，然而直接状压是会$T$飞的，最多只能拿到$80PTS$

所以这时我们要引出一个新的状压技巧—轮廓线状压

所谓轮廓线状压，顾名思义就是状压一条线

如下图所示，假设我们要更新绿色格点对答案的影响，我们之前状压的就是红色的这条线，接下来我们根据题目的具体规则进行刷表转移，枚举这个绿色格点的所有可能取值，然后更新到蓝色格点即可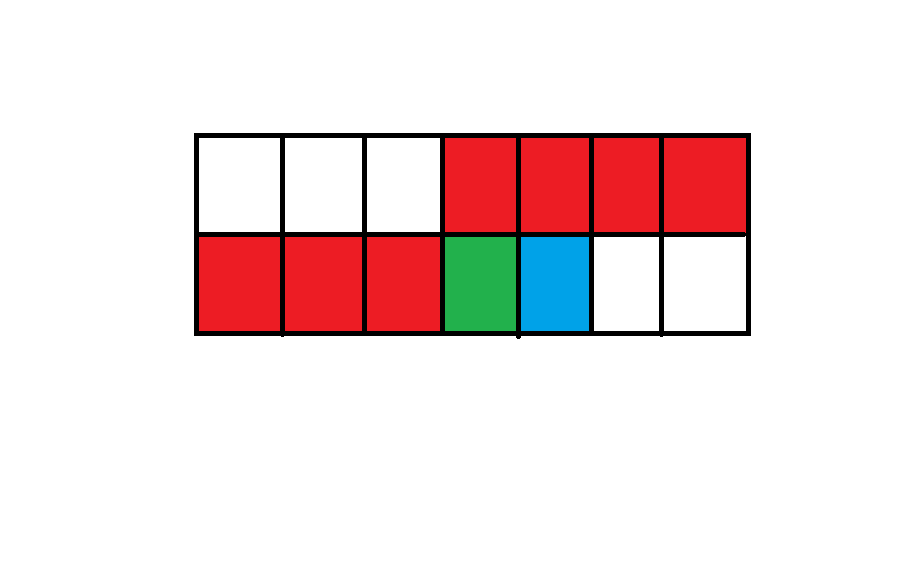

需要注意的是每个格点只能更新到与他相邻的下一个格点，那么我们每次只能向一个状态更新，再算上这次使用的状态一共就是两个状态，所以这里可以用滚动数组优化掉一维$DP$状态

具体的对于这个题而言我们枚举当前格点的颜色如果和它相邻的格点和它颜色不一样那么就可以把它的影响加入答案并且更新到下一个格点的状态

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
#define re register 
#define ll long long
const ll MOD=376544743;
int n,m,k,head,tail;
int answer,dp[2][50000050];
int mi[15];
int read()
{
    int s=0,p=1;
    char st=getchar();
    while(st<'0' || st>'9')
    {
        if(st=='-')p=-1;
        st=getchar();
    }
    while(st>='0' && st<='9')
    {
        s=(s<<1)+(s<<3)+(st^48);
        st=getchar();
    }
    return s*p;
}
int find(int x,int j)
{
    return (x/mi[j-1])%k;
}
int change(int x,int j,int y)
{
    return x-find(x,j)*mi[j-1]+y*mi[j-1];
}
void print(int x)
{
    for(int i=1;i<=m;i++)cout<<x%k,x/=k;
}
int ch(int a)
{
    int last,now;
    last=a%k;
    a=a/k;
    for(int i=1;i<=m-1;i++)
    {
        now=a%k;
        if(last==now)return 0;
        last=now;
        a=a/k;
    }
    return 1;
}
int main()
{
    n=read();m=read();k=read();
    int x;
    for(int i=1;i<=m;i++)x=read(),head=(head*k)+x;
    for(int i=1;i<=m;i++)x=read(),tail=(tail*k)+x;
    if(k==2)
    {
        if(n%2==0)
        {
            if(head==tail)cout<<0;
            else cout<<1;
        }
        else 
        {
            if(head==tail)cout<<1;
            else cout<<0;
        }
        return 0;
    }
    mi[0]=1;
    for(int i=1;i<=m;i++)mi[i]=mi[i-1]*k;
    dp[1][head]=1;
    int r=0;
    int all=mi[m];
    for(int i=2;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            r=r^1;
            for(int d=0;d<all;d++)dp[r^1][d]=0;
            for(int d=0;d<all;d++)
            {
                if(dp[r][d]==0)continue;
                int lll;
                int rr=find(d,j);
                lll=-1;
                if(j-1>0)lll=find(d,j-1);
                for(int p=0;p<=k-1;p++)if(p!=lll && p!=rr)(dp[r^1][change(d,j,p)]+=dp[r][d])%=MOD;
            }
        }
    printf("%d",dp[r^1][tail]%MOD);
    return 0;
}